This is default featured slide 1 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 2 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 3 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 4 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
This is default featured slide 5 title
Go to Blogger edit html and find these sentences.Now replace these sentences with your own descriptions.
Jumat, 06 Desember 2013
contoh soal vektor
Soal No. 1
Diberikan dua buah vektor gaya yang sama besar masing-masing vektor besarnya adalah 10 Newton seperti gambar berikut.
Diberikan dua buah vektor gaya yang sama besar masing-masing vektor besarnya adalah 10 Newton seperti gambar berikut.

Jika sudut yang terbentuk antara kedua vektor adalah 60°, tentukan nilai resultan kedua vektor!
Pembahasan
Resultan untuk dua buah vektor yang telah diketahui sudutnya
Resultan untuk dua buah vektor yang telah diketahui sudutnya
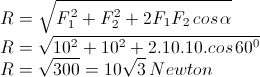
Soal No. 2
Dua buah vektor kecepatan P dan Q masing-masing besarnya 40 m/s dan 20 m/s membentuk sudut 60°.

Tentukan selisih kedua vektor tersebut!
Pembahasan
Menentukan selisih dua buah vektor yang diketahui sudutnya:
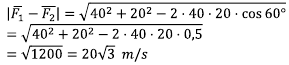
Soal No. 3
Dua buah vektor gaya masing – masing 8 N dan 4 N saling mengapit sudut 120°. Tentukan besar resultan kedua vektor tersebut!
Pembahasan
Data:
F1 = 8 N
F2 = 4 N
α = 120°
R = ........

Catatan rumus:
cos (180° − α) = − cos α
Sehingga untuk nilai cos 120°:
cos 120° = cos (180° − 60°) = − cos 60° = − 1/2
Soal No. 4
Perhatikan gambar berikut!

Jika satu kotak mewakili 10 Newton, tentukan resultan antara kedua vektor!
Pembahasan
Cari jumlah resultan pada sumbu x dan sumbu y, cukup dengan menghitung kotak dari masing-masing vektor, F1 adalah 30 ke kanan, 40 ke atas, sementara F2 adalah 50 ke kanan, 20 ke atas, kemudian masukkan rumus resultan:
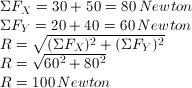
Soal No. 5
Diberikan 3 buah vektor F1=10 N, F2 =25 N dan F3=15 N seperti gambar berikut.
Diberikan 3 buah vektor F1=10 N, F2 =25 N dan F3=15 N seperti gambar berikut.

Tentukan:
a. Resultan ketiga vektor
a. Resultan ketiga vektor
b. Arah resultan terhadap sumbu X
[Sin 37° = (3/5), Sin 53° = (4/5)]
[Cos 37° = (4/5), Cos 53° = (3/5)]
Pembahasan
a. Ikuti langkah-langkah berikut:
1. Uraikan semua vektor ke sumbu x dan sumbu y (kecuali vektor yang sudah lurus pada sumbu x atau y seperti F2). Lihat gambar di bawah!
2. Cari jumlah vektor pada sumbu x ( kanan +, kiri -)
3. Cari jumlah vektor pada sumbu y (atas +, bawah -)
4. Masukkan rumus resultan

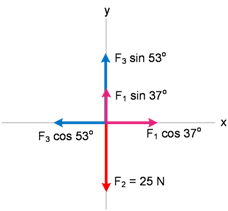
Jumlah komponen vektor-vektor pada sumbu x dan y :

b. Mencari sudut yang terbentuk antara resultan vektor R dengan sumbu x
tan θ = ΣFy /ΣFx
tan θ = −7/−1 = 7
θ = arc. tan 7 = 81,87°
Thanks to PCP http://journalputrika.blogspot.com atas koreksinya :-)
Soal No. 6
Ditentukan 2 buah vektor F yang sama besarnya. Bila perbandingan antara besar jumlah dan besar selisih kedua vektor sama dengan √3, tentukan besar sudut yang dibentuk oleh kedua vektor! (Sumber Soal : SPMB)
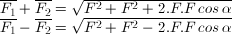
Perbandingan jumlah dan selisihnya adalah √3 sehingga:
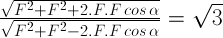
Kuadratkan ruas kiri dan kanan
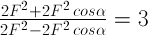
Kali silang :
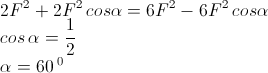
Soal No. 7
Sebuah perahu menyeberangi sungai yang lebarnya 180 m dan kecepatan airnya 4 m/s. Bila perahu diarahkan menyilang tegak lurus dengan kecepatan 3 m/s, tentukan panjang lintasan yang ditempuh perahu hingga sampai ke seberang sungai! (Sumber Soal : UMPTN)
Ditentukan 2 buah vektor F yang sama besarnya. Bila perbandingan antara besar jumlah dan besar selisih kedua vektor sama dengan √3, tentukan besar sudut yang dibentuk oleh kedua vektor! (Sumber Soal : SPMB)
Pembahasan
Jumlah dan selisih kedua vektor masing-masing adalah:
Perbandingan jumlah dan selisihnya adalah √3 sehingga:
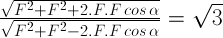
Kuadratkan ruas kiri dan kanan
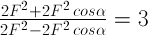
Kali silang :
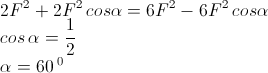
Soal No. 7
Sebuah perahu menyeberangi sungai yang lebarnya 180 m dan kecepatan airnya 4 m/s. Bila perahu diarahkan menyilang tegak lurus dengan kecepatan 3 m/s, tentukan panjang lintasan yang ditempuh perahu hingga sampai ke seberang sungai! (Sumber Soal : UMPTN)

Pembahasan
Asumsikan bahwa perahu bergerak lurus beraturan
menempuh lintasan AD dan resultan kecepatan perahu dan air adalah 5 m/s
(gunakan aturan Phytagoras). Dengan membandingkan sisi-sisi segitiga ABC
dan ADE :

Tips
"Untuk dua buah vektor dengan besar yang sama dan membentuk sudut 120o maka resultan kedua vektor besarnya akan sama dengan besar salah satu vektor"
Berikut ilustrasinya:
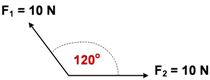
Dua buah vektor dengan besar yang sama yaitu 10 N membentuk sudut 120o maka nilai resultan kedua vektor juga 10 N.

Berikut contoh soal diambil dari soal EBTANAS (UN tempo dulu, zaman kakak-kakak kita) tahun 2000.
Perhatikan gambar gaya-gaya di bawah ini!

Besar resultan ketiga gaya tersebut adalah....
A. 2,0 N
B. 2 √3 N
C. 3,0 N
D. 3 √3 N
E. 4√3 N
Pada soal di atas 2 buah vektor (gaya) 3 N membentuk sudut 120o,
sehingga resultan kedua gaya juga 3 N. Resultan kedua gaya ini akan
segaris dengan gaya 6 N, namun berlawanan arah. Sehingga dengan mudah
soal ini bisa dijawab resultan ketiga gaya adalah 6 N dikurangi 3 N
hasilnya adalah 3 N.
Soal No. 8
Diberikan 3 buah vektor :
a = 2i + 3j satuan
b = 4i + 5j satuan
c = 6i + 7j satuan
Tentukan besar resultan ketiga vektor, dan kemiringan sudut antara resultan dan sumbu X
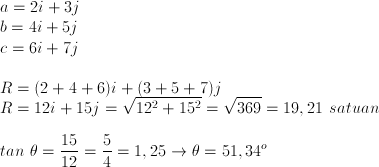
Soal No. 8
Diberikan 3 buah vektor :
a = 2i + 3j satuan
b = 4i + 5j satuan
c = 6i + 7j satuan
Tentukan besar resultan ketiga vektor, dan kemiringan sudut antara resultan dan sumbu X
Data:
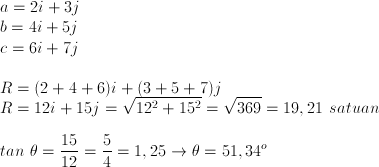
Untuk lebih jelas berikut ilustrasinya:

12 pada sumbu x
15 pada sumbu y
Arahnya adalah sudut θ yang bisa dicari dari sin θ, cos θ maupun tan θ. Jika dicari dari tan θ maka yang dibandingkan nilai pada sumbu y dengan nilai pada sumbu x. Jika dicari dari sin θ yang dibandingkan nilai pada sumbu y dengan nilai resultan R, jika digunakan cos θ bandingkan nilai pada sumbu x dengan nilai resultan R. Soal No. 9
Diberikan 3 buah vektor a, b, c seperti gambar di bawah.

Dengan metode poligon tunjukkan :
(i) d = a + b + c
(ii) d = a + b − c
(iii) d = a − b + c
(i) d = a + b + c
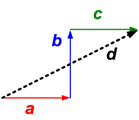
(ii) d = a + b − c
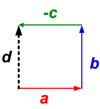
(iii) d = a − b + c

Soal No. 10
Diberikan dua buah vektor masing-masing vektor dan besarnya adalah A = 8 satuan, B = 10 satuan. Kedua vektor ini membentuk sudut 37°. Tentukan hasil dari:
a) A⋅ B
b) A × B
Pembahasan
a) A⋅ B adalah perkalian titik (dot) antara vektor A dan vektor B
Untuk perkalian titik berlaku
A⋅ B = A B cos θ
Sehingga
A⋅ B = A B cos 37° = (8)(10)(0,8) = 64 satuan
b) A × B adalah perkalian silang (cross) vektor A dan vektor B
Untuk perkalian silang berlaku
A × B = A B sin θ
Sehingga
A × B = A B sin 37° = (8)(10)(0,6) = 48 satuan

12 pada sumbu x
15 pada sumbu y
Arahnya adalah sudut θ yang bisa dicari dari sin θ, cos θ maupun tan θ. Jika dicari dari tan θ maka yang dibandingkan nilai pada sumbu y dengan nilai pada sumbu x. Jika dicari dari sin θ yang dibandingkan nilai pada sumbu y dengan nilai resultan R, jika digunakan cos θ bandingkan nilai pada sumbu x dengan nilai resultan R. Soal No. 9
Diberikan 3 buah vektor a, b, c seperti gambar di bawah.

Dengan metode poligon tunjukkan :
(i) d = a + b + c
(ii) d = a + b − c
(iii) d = a − b + c
Pembahasan
Dengan metode poligon :(i) d = a + b + c

(ii) d = a + b − c

(iii) d = a − b + c

Soal No. 10
Diberikan dua buah vektor masing-masing vektor dan besarnya adalah A = 8 satuan, B = 10 satuan. Kedua vektor ini membentuk sudut 37°. Tentukan hasil dari:
a) A⋅ B
b) A × B
Pembahasan
a) A⋅ B adalah perkalian titik (dot) antara vektor A dan vektor B
Untuk perkalian titik berlaku
A⋅ B = A B cos θ
Sehingga
A⋅ B = A B cos 37° = (8)(10)(0,8) = 64 satuan
b) A × B adalah perkalian silang (cross) vektor A dan vektor B
Untuk perkalian silang berlaku
A × B = A B sin θ
Sehingga
A × B = A B sin 37° = (8)(10)(0,6) = 48 satuan
Read more: http://fisikastudycenter.com/fisika-x-sma/5-vektor#ixzz2mgN8dNiZ
contoh soal GLBB dan GLB
Soal No. 1
Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.

Jika percepatan gravitasi ditempat tersebut adalah 10 m/s2, dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah
Pembahasan
a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:

b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:

c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
Soal No. 2
Sebuah mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan nilai perlambatan yang diberikan pada mobil tersebut!
Pembahasan
Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:
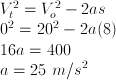
Soal No. 3
Perhatikan grafik berikut ini.

Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.
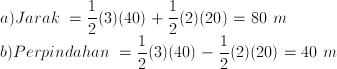
Soal No. 4
Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.
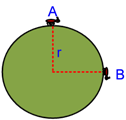
Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
Pembahasan
Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak = 1/4 (2πr) = 1/4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 22 + 22 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
Soal No. 5
Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.

Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
Pembahasan
Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR

PQ = VPQ x tPQ = (200 km/jam) x (0,5) jam = 100 km
QR = VQR x tQR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53o = (100 km) x (0,6) = 60 km
RR' = QR sin 53o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )2 + (RR')2 ]
PR = √[ (160 ) 2 + (80)2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
Soal No. 6
Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:

Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
Pembahasan
Mencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) = 2/3 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) = 3/2 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
Soal No. 7
Dari gambar berikut :

Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasan
a) Jarak tempuh dari A - B
Cara Pertama
Data :
Vo = 0 m/s
a = (2 − 0) : (3− 0) = 2/3 m/s2
t = 3 sekon
S = Vo t + 1/2 at2
S = 0 + 1/2 (2/3 )(3)2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
Vo = 2 m/s
a = 3/2 m/s2
t = 9 − 7 = 2 sekon
S = Vo t + 1/2 at2
S = (2)(2) + 1/2 (3/2 )(2)2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
Soal No. 8
Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.

Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing VA = 40 m/s dan VB = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)
tA = tB
SA/VA = SB/VB
( x )/40 = ( 1200 − x ) /60
6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = VA t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
SB =VB t = (60) (12) = 720 m
Soal No. 9
Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.

Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
Pembahasan
Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s2
Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
SA = SB
VA t =VoB t + 1/2 at2
80t = (0)t + 1/2 (4)t2
2t2 − 80t = 0
t2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
SA = VA t = (80)(40) = 3200 meter
Soal No. 10 (Gerak Vertikal ke Bawah / Jatuh Bebas)
Sebuah benda jatuh dari ketinggian 100 m. Jika percepatan gravitasi bumi 10 m/s2 tentukan:
a) kecepatan benda saat t = 2 sekon
b) jarak tempuh benda selama 2 sekon
c) ketinggian benda saat t = 2 sekon
d) kecepatan benda saat tiba di tanah
e) waktu yang diperlukan benda hingga tiba di tanah
Pembahasan
a) kecepatan benda saat t = 2 sekon
Data :
t = 2 s
a = g = 10 m/s2
Vo = 0 m/s
Vt = .....!
Vt = Vo + at
Vt = 0 + (10)(2) = 20 m/s
c) jarak tempuh benda selama 2 sekon
S = Vot + 1/2at2
S = (0)(t) + 1/2 (10)(2)2
S = 20 meter
c) ketinggian benda saat t = 2 sekon
ketinggian benda saat t = 2 sekon adalah tinggi mula-mula dikurangi jarak yang telah ditempuh benda.
S = 100 − 20 = 80 meter
d) kecepatan benda saat tiba di tanah
Vt2 = Vo2 + 2aS
Vt2 = (0) + 2 aS
Vt = √(2aS) = √[(2)(10)(100)] = 20√5 m/s
e) waktu yang diperlukan benda hingga tiba di tanah
Vt = V0 + at
20√5 = (0) + (10) t
t = 2√5 sekon
Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.

Jika percepatan gravitasi ditempat tersebut adalah 10 m/s2, dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah
Pembahasan
a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:

b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:

c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
Soal No. 2
Sebuah mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan nilai perlambatan yang diberikan pada mobil tersebut!
Pembahasan
Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:
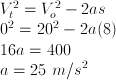
Soal No. 3
Perhatikan grafik berikut ini.

Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.
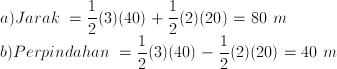
Soal No. 4
Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.

Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
Pembahasan
Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak = 1/4 (2πr) = 1/4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 22 + 22 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
Soal No. 5
Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.

Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
Pembahasan
Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR

PQ = VPQ x tPQ = (200 km/jam) x (0,5) jam = 100 km
QR = VQR x tQR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53o = (100 km) x (0,6) = 60 km
RR' = QR sin 53o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )2 + (RR')2 ]
PR = √[ (160 ) 2 + (80)2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
Soal No. 6
Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:

Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
Pembahasan
Mencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) = 2/3 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) = 3/2 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
Soal No. 7
Dari gambar berikut :

Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasan
a) Jarak tempuh dari A - B
Cara Pertama
Data :
Vo = 0 m/s
a = (2 − 0) : (3− 0) = 2/3 m/s2
t = 3 sekon
S = Vo t + 1/2 at2
S = 0 + 1/2 (2/3 )(3)2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
Vo = 2 m/s
a = 3/2 m/s2
t = 9 − 7 = 2 sekon
S = Vo t + 1/2 at2
S = (2)(2) + 1/2 (3/2 )(2)2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
Soal No. 8
Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.

Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing VA = 40 m/s dan VB = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)
tA = tB
SA/VA = SB/VB
( x )/40 = ( 1200 − x ) /60
6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = VA t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
SB =VB t = (60) (12) = 720 m
Soal No. 9
Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.

Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
Pembahasan
Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s2
Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
SA = SB
VA t =VoB t + 1/2 at2
80t = (0)t + 1/2 (4)t2
2t2 − 80t = 0
t2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
SA = VA t = (80)(40) = 3200 meter
Soal No. 10 (Gerak Vertikal ke Bawah / Jatuh Bebas)
Sebuah benda jatuh dari ketinggian 100 m. Jika percepatan gravitasi bumi 10 m/s2 tentukan:
a) kecepatan benda saat t = 2 sekon
b) jarak tempuh benda selama 2 sekon
c) ketinggian benda saat t = 2 sekon
d) kecepatan benda saat tiba di tanah
e) waktu yang diperlukan benda hingga tiba di tanah
Pembahasan
a) kecepatan benda saat t = 2 sekon
Data :
t = 2 s
a = g = 10 m/s2
Vo = 0 m/s
Vt = .....!
Vt = Vo + at
Vt = 0 + (10)(2) = 20 m/s
c) jarak tempuh benda selama 2 sekon
S = Vot + 1/2at2
S = (0)(t) + 1/2 (10)(2)2
S = 20 meter
c) ketinggian benda saat t = 2 sekon
ketinggian benda saat t = 2 sekon adalah tinggi mula-mula dikurangi jarak yang telah ditempuh benda.
S = 100 − 20 = 80 meter
d) kecepatan benda saat tiba di tanah
Vt2 = Vo2 + 2aS
Vt2 = (0) + 2 aS
Vt = √(2aS) = √[(2)(10)(100)] = 20√5 m/s
e) waktu yang diperlukan benda hingga tiba di tanah
Vt = V0 + at
20√5 = (0) + (10) t
t = 2√5 sekon
contoh soal listrik dinamis
Soal No. 1
Dalam waktu dua menit arus listrik sebesar 2 A mengalir sepanjang kawat penghantar. Tentukan:
a) muatan yang berpindah
b) jumlah elektron
Pembahasan
Hubungan kuat arus listrik, muatan listrik dan waktu adalah:
I = Q / t
Q = I x t
Dengan demikian :
a) Q = I x t
Q = 2 x 120
Q = 240 Coulomb
b) menentukan jumlah elektron dalam muatan
n = Q/Qe
dimana:
n = jumlah elektron
Qe = muatan satu elektron (1,6 x 10−19 Coulomb)
Q = muatan yang akan dihitung jumlah elektronnya
sehingga:
n = Q/Qe
n = 240 / (1,6 x 10−19)
n = 150 x 1019
n = 1,5 x 1021 buah elektron
Soal No. 5
Sebuah kawat penghantar memiliki panjang L dan luas penampang A dan memiliki hambatan sebesar 120 Ω. Jika kawat dengan bahan yang sama memiliki panjang 2 L dan luas penampang 3 A, tentukan hambatan kawat kedua ini!
Pembahasan
Rumus untuk menghitung hambatan suatu kawat penghantar adalah:
R = ρL/ A
dimana
R = hambatan kawat (Ω)
L = panjang kawat (m)
A = luas penampang kawat (m2)
ρ = hambat jenis kawat
Kawat yang berbahan sama memiliki hambat jenis yang sama, sehingga
R2 / R1 = (L2/A2) / (L1/A1)
R2 = (L2/L1) x (A1/A2) x R1
R2 = (2L/L) x (A/3A) x 120
R2 = (2/1) x(1/3)
R2 = (2/3) x 120 = 80 Ω
Soal No. 2
Muatan sebesar 360 C mengalir dalam dua menit dalam suatu rangkaian. Tentukan Kuat arus rangkaian listrik tersebut!
Pembahasan
I = Q/t
I = 360 coulomb / 120 sekon
I = 3 Ampere
Soal No. 3
Konversikan satuan berikut:
a) 5 μ C = ........C
b) 100 mC = .........C
c) 5000 nC = .........C
Pembahasan
a) 5 μC = 5 x 10−6 = 0,000005 C
b) 100 mC = 100 x 10−3 = 0,1 C
c) 5000 nC = 5000 x 10−9 = 5 x 10−6 = 0,000005 C
Soal No. 4
Konversikan satuan berikut :
a) 5 kΩ = ....... Ω
b) 0,3 kΩ = .....Ω
c) 5 MΩ = .........Ω
Pembahasan
a) 5 kΩ = 5 x 1000 = 5000 Ω
b) 0,3 kΩ = 0,3 x 1000 = 300 Ω
c) 5 MΩ = 5 x 1000000 = 5000000 Ω
Soal No. 6
Sebuah kawat penghantar dengan panjang 10 meter memiliki hambatan sebesar 100 Ω Jika kawat dipotong menjadi 2 bagian yang sama panjang, tentukan hambatan yang dimiliki oleh masing-masing potongan kawat!
Pembahasan
Data dari soal:
L1 = L
L2 = 1/2 L
A1 = A2
R1 = 100 Ω
R2 / R1 = (L2/L1) x R1
(luas penampang dan hambat jenis kedua kawat adalah sama!!)
R2 = ( 0,5 L / L) x 100 Ω:
R2 = 50 Ω (Thanks to nasha atas masukannya,..)
Soal No. 7
Ubah satuan berikut:
a) 300 mA = .........A
b) 12 mA = ..........A
Pembahasan
a) 300 mA = 300 : 1000 = 0,3 A
b) 12 mA = 12 : 1000 = 0,012 A
Soal No. 8
Diberikan sebuah rangkaian listrik arus searah terdiri dari tiga buah lampu, dua buah saklar dan sebuah sumber arus listrik. Manakah lampu-lampu yang menyala jika:
a) saklar 1 tertutup, saklar 2 terbuka
b) saklar 2 tertutup, saklar 1 terbuka
c) saklar 1 tertutup, saklar 2 tertutup
d) saklar 1 terbuka, saklar 2 terbuka

Pembahasan
Arus listrik akan mengalir jika terdapat beban dan rangkaian yang tertutup, sehingga:
a) saklar 1 tertutup, saklar 2 terbuka
lampu 2 dan 3 menyala, lampu 1 mati
b) saklar 2 tertutup, saklar 1 terbuka
semua lampu akan mati
c) saklar 1 tertutup, saklar 2 tertutup
semua lampu menyala
d) saklar 1 terbuka, saklar 2 terbuka
semua lampu mati
Soal No. 9
X dan Y adalah dua buah alat ukur listrik yang berbeda. Manakah posisi pemasangan voltmeter dan amperemeter jika yang diukur adalah tegangan pada lampu 3 dan kuat arus pada lampu 3?

Pembahasan
Voltmeter untuk mengukur tegangan antara dua titik, dalam hal ini adalah tegangan pada lampu 3, voltmeter harus dipasang secara paralel dengan beban yang hendak diukur, posisi yang benar adalah X.
Amperemeter untuk mengukur kuat arus yang mengalir melalui suatu beban dalam hal ini adalah lampu 3, ampermeter harus dipasang secara seri dengan alat yang hendak diukur besar kuat arusnya, so, kabelnya dipotong dulu trus sambungin ke kaki Amperemeter, posisi yang benar adalah Y.
Soal No. 10
Perhatikan gambar berikut

Tentukan hambatan pengganti antara titik A dan B jika R1, R2 dan R3 berturut-turut besarnya adalah 5 Ω, 10 Ω dan 15 Ω!
Pembahasan
Rangkaian diatas adalah tersusun seri, sehingga hambatan penggantinya adalah:
Rt = R1 + R2 + R3
= 5 + 10 + 15
= 30 Ω
Read more: http://fisikastudycenter.com/fisika-smp/244-listrik-dinamis-kelas-9-smp-part-1#ixzz2mgMCm37n
Dalam waktu dua menit arus listrik sebesar 2 A mengalir sepanjang kawat penghantar. Tentukan:
a) muatan yang berpindah
b) jumlah elektron
Pembahasan
Hubungan kuat arus listrik, muatan listrik dan waktu adalah:
I = Q / t
Q = I x t
Dengan demikian :
a) Q = I x t
Q = 2 x 120
Q = 240 Coulomb
b) menentukan jumlah elektron dalam muatan
n = Q/Qe
dimana:
n = jumlah elektron
Qe = muatan satu elektron (1,6 x 10−19 Coulomb)
Q = muatan yang akan dihitung jumlah elektronnya
sehingga:
n = Q/Qe
n = 240 / (1,6 x 10−19)
n = 150 x 1019
n = 1,5 x 1021 buah elektron
Soal No. 5
Sebuah kawat penghantar memiliki panjang L dan luas penampang A dan memiliki hambatan sebesar 120 Ω. Jika kawat dengan bahan yang sama memiliki panjang 2 L dan luas penampang 3 A, tentukan hambatan kawat kedua ini!
Pembahasan
Rumus untuk menghitung hambatan suatu kawat penghantar adalah:
R = ρL/ A
dimana
R = hambatan kawat (Ω)
L = panjang kawat (m)
A = luas penampang kawat (m2)
ρ = hambat jenis kawat
Kawat yang berbahan sama memiliki hambat jenis yang sama, sehingga
R2 / R1 = (L2/A2) / (L1/A1)
R2 = (L2/L1) x (A1/A2) x R1
R2 = (2L/L) x (A/3A) x 120
R2 = (2/1) x(1/3)
R2 = (2/3) x 120 = 80 Ω
Soal No. 2
Muatan sebesar 360 C mengalir dalam dua menit dalam suatu rangkaian. Tentukan Kuat arus rangkaian listrik tersebut!
Pembahasan
I = Q/t
I = 360 coulomb / 120 sekon
I = 3 Ampere
Soal No. 3
Konversikan satuan berikut:
a) 5 μ C = ........C
b) 100 mC = .........C
c) 5000 nC = .........C
Pembahasan
a) 5 μC = 5 x 10−6 = 0,000005 C
b) 100 mC = 100 x 10−3 = 0,1 C
c) 5000 nC = 5000 x 10−9 = 5 x 10−6 = 0,000005 C
Soal No. 4
Konversikan satuan berikut :
a) 5 kΩ = ....... Ω
b) 0,3 kΩ = .....Ω
c) 5 MΩ = .........Ω
Pembahasan
a) 5 kΩ = 5 x 1000 = 5000 Ω
b) 0,3 kΩ = 0,3 x 1000 = 300 Ω
c) 5 MΩ = 5 x 1000000 = 5000000 Ω
Soal No. 6
Sebuah kawat penghantar dengan panjang 10 meter memiliki hambatan sebesar 100 Ω Jika kawat dipotong menjadi 2 bagian yang sama panjang, tentukan hambatan yang dimiliki oleh masing-masing potongan kawat!
Pembahasan
Data dari soal:
L1 = L
L2 = 1/2 L
A1 = A2
R1 = 100 Ω
R2 / R1 = (L2/L1) x R1
(luas penampang dan hambat jenis kedua kawat adalah sama!!)
R2 = ( 0,5 L / L) x 100 Ω:
R2 = 50 Ω (Thanks to nasha atas masukannya,..)
Soal No. 7
Ubah satuan berikut:
a) 300 mA = .........A
b) 12 mA = ..........A
Pembahasan
a) 300 mA = 300 : 1000 = 0,3 A
b) 12 mA = 12 : 1000 = 0,012 A
Soal No. 8
Diberikan sebuah rangkaian listrik arus searah terdiri dari tiga buah lampu, dua buah saklar dan sebuah sumber arus listrik. Manakah lampu-lampu yang menyala jika:
a) saklar 1 tertutup, saklar 2 terbuka
b) saklar 2 tertutup, saklar 1 terbuka
c) saklar 1 tertutup, saklar 2 tertutup
d) saklar 1 terbuka, saklar 2 terbuka

Pembahasan
Arus listrik akan mengalir jika terdapat beban dan rangkaian yang tertutup, sehingga:
a) saklar 1 tertutup, saklar 2 terbuka
lampu 2 dan 3 menyala, lampu 1 mati
b) saklar 2 tertutup, saklar 1 terbuka
semua lampu akan mati
c) saklar 1 tertutup, saklar 2 tertutup
semua lampu menyala
d) saklar 1 terbuka, saklar 2 terbuka
semua lampu mati
Soal No. 9
X dan Y adalah dua buah alat ukur listrik yang berbeda. Manakah posisi pemasangan voltmeter dan amperemeter jika yang diukur adalah tegangan pada lampu 3 dan kuat arus pada lampu 3?

Pembahasan
Voltmeter untuk mengukur tegangan antara dua titik, dalam hal ini adalah tegangan pada lampu 3, voltmeter harus dipasang secara paralel dengan beban yang hendak diukur, posisi yang benar adalah X.
Amperemeter untuk mengukur kuat arus yang mengalir melalui suatu beban dalam hal ini adalah lampu 3, ampermeter harus dipasang secara seri dengan alat yang hendak diukur besar kuat arusnya, so, kabelnya dipotong dulu trus sambungin ke kaki Amperemeter, posisi yang benar adalah Y.
Soal No. 10
Perhatikan gambar berikut

Tentukan hambatan pengganti antara titik A dan B jika R1, R2 dan R3 berturut-turut besarnya adalah 5 Ω, 10 Ω dan 15 Ω!
Pembahasan
Rangkaian diatas adalah tersusun seri, sehingga hambatan penggantinya adalah:
Rt = R1 + R2 + R3
= 5 + 10 + 15
= 30 Ω
Read more: http://fisikastudycenter.com/fisika-smp/244-listrik-dinamis-kelas-9-smp-part-1#ixzz2mgMCm37n
contoh soal gaya gravitasi
Soal No. 1
Diketahui percepatan gravitasi di sebuah tempat pada permukaan bumi sebesar 10 m/s2. Jika R adalah jari-jari bumi, tentukan percepatan gravitasi bumi pada tempat yang berjarak 2R dari pusat bumi!
Pembahasan
Data dari soal di atas:
r1 = R
r2 = 2R
g1 = 10 m/s2
g2 = ..................
Rumus percepatan gravitasi:

Dari data soal

Soal No. 2
Diketahui percepatan gravitasi di sebuah tempat pada permukaan bumi sebesar 10 m/s2. Jika R adalah jari-jari bumi, tentukan percepatan gravitasi bumi pada tempat yang berjarak 0,5 R dari permukaan bumi!
Pembahasan
Data dari soal di atas:
r1 = R
r2 = (R + 0,5 R) = 1,5 R
g1 = 10 m/s2
g2 = ..................
Dengan rumus yang sama dengan soal nomor 1

Dari data soal

Soal No. 3
Titik C berada di antara dua buah planet seperti berikut!

Planet A memiliki massa 16 M dan planet B memiliki massa 25 M. Tentukan letak titik C dari planet A agar pengaruh medan grafitasi kedua planet sebesar nol!
Pembahasan
Agar nol, maka pengaruh gravitasi dari planet A dan dari planet B sama besar dan berlawanan arah.

gA = gB

Masukkan nilai m masing-masingl

Akarkan kiri, akarkan kanan kemudian kalikan silang

Soal No. 4
Titik A, B dan C terletak dalam medan gravitasi bumi seperti pada gambar!

Diketahui M = massa bumi, R = jari-jari bumi. Kuat medan gravitasi di titik A sama dengan g (N.kg−1 ) Perbandingan kuat medan gravitasi di titik A dan titik C adalah....
A. 3 : 8
B. 4 : 1
C. 8 : 1
D. 8 : 3
E. 9 : 1
(Medan Gravitasi - UN Fisika 2010)
Soal No. 5
Jika diambil massa Bumi = 81 kali massa bulan, dan jarak Bumi - Bulan = a, maka jarak titik netral, r (titik dimana gaya gravitasi yang berasal dari Bulan dan yang berasal dari Bumi sama besarnya), adalah....
A. r = 0,9 a
B. r = 0,8 a
C. r = 0,7 a
D. r = 0,6 a
E. r = 0,5 a
(Medan Gravitasi - Olimpiade astronomi 2008)
Pembahasan
Seperti soal nomor 3. Jarak titik netral adalah r.

Sehingga sisa jaraknya adalah (a - r). Misalkan massa bulan adalah m, maka massa bumi adalah 81 m.

Read more: http://fisikastudycenter.com/fisika-xi-sma/323-percepatan-gravitasi-bumi-planet#ixzz2mgLbBs1W
Diketahui percepatan gravitasi di sebuah tempat pada permukaan bumi sebesar 10 m/s2. Jika R adalah jari-jari bumi, tentukan percepatan gravitasi bumi pada tempat yang berjarak 2R dari pusat bumi!
Pembahasan
Data dari soal di atas:
r1 = R
r2 = 2R
g1 = 10 m/s2
g2 = ..................
Rumus percepatan gravitasi:

Dari data soal

Soal No. 2
Diketahui percepatan gravitasi di sebuah tempat pada permukaan bumi sebesar 10 m/s2. Jika R adalah jari-jari bumi, tentukan percepatan gravitasi bumi pada tempat yang berjarak 0,5 R dari permukaan bumi!
Pembahasan
Data dari soal di atas:
r1 = R
r2 = (R + 0,5 R) = 1,5 R
g1 = 10 m/s2
g2 = ..................
Dengan rumus yang sama dengan soal nomor 1

Dari data soal

Soal No. 3
Titik C berada di antara dua buah planet seperti berikut!

Planet A memiliki massa 16 M dan planet B memiliki massa 25 M. Tentukan letak titik C dari planet A agar pengaruh medan grafitasi kedua planet sebesar nol!
Pembahasan
Agar nol, maka pengaruh gravitasi dari planet A dan dari planet B sama besar dan berlawanan arah.

gA = gB

Masukkan nilai m masing-masingl

Akarkan kiri, akarkan kanan kemudian kalikan silang

Soal No. 4
Titik A, B dan C terletak dalam medan gravitasi bumi seperti pada gambar!

Diketahui M = massa bumi, R = jari-jari bumi. Kuat medan gravitasi di titik A sama dengan g (N.kg−1 ) Perbandingan kuat medan gravitasi di titik A dan titik C adalah....
A. 3 : 8
B. 4 : 1
C. 8 : 1
D. 8 : 3
E. 9 : 1
(Medan Gravitasi - UN Fisika 2010)
Soal No. 5
Jika diambil massa Bumi = 81 kali massa bulan, dan jarak Bumi - Bulan = a, maka jarak titik netral, r (titik dimana gaya gravitasi yang berasal dari Bulan dan yang berasal dari Bumi sama besarnya), adalah....
A. r = 0,9 a
B. r = 0,8 a
C. r = 0,7 a
D. r = 0,6 a
E. r = 0,5 a
(Medan Gravitasi - Olimpiade astronomi 2008)
Pembahasan
Seperti soal nomor 3. Jarak titik netral adalah r.

Sehingga sisa jaraknya adalah (a - r). Misalkan massa bulan adalah m, maka massa bumi adalah 81 m.

Read more: http://fisikastudycenter.com/fisika-xi-sma/323-percepatan-gravitasi-bumi-planet#ixzz2mgLbBs1W
Langganan:
Komentar (Atom)

















